“Masonry beam construction” after roof breaking
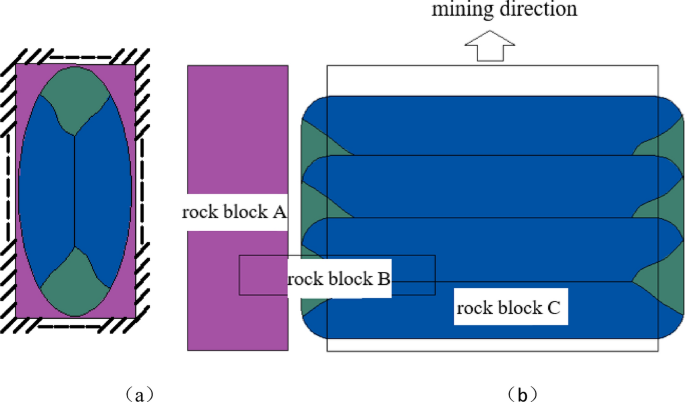
With the continual development of the working face, the overburden rock within the goaf will lose the unique supporting situations. Presently, the roof of the goaf is pressure-bearing for a very long time underneath the continual loading of the overburden rock. Within the technique of advancing the working face, solely the false roof will collapse, and different roofs are nonetheless in a suspended state. The suspended roof might be considered a four-sided fastened plate. When the uncollapsed roof reaches the restrict span, it first breaks in the course of the lengthy aspect of the roof, after which cracks are fashioned in the course of the brief aspect. After all of the cracks penetrate, the “O” -shaped injury is fashioned, ensuing within the preliminary fracture of the “X” form. With the mining advance of the working face, the “Ok”-shaped periodic collapse shall be fashioned after a number of collapses, and the roof state adjustments to 3 sides fastened and one aspect merely supported plate. In keeping with the horizontal power of mutual extrusion of damaged rock, friction is generated between rock blocks. The working face might be divided into three areas: higher, center, and decrease. The higher and decrease areas of the working face type an arc-shaped failure underneath the motion of friction. The rock blocks belong to a three-dimensional occlusion relationship. Within the center space, a beam-like look is fashioned, which is basically an arched fractured beam construction, known as a “masonry beam”, as proven in Fig. 230,31.
Roof breaking and caving type.
In keeping with the “masonry beam” construction mannequin of the overburden rock, the important thing strata of the overburden rock are divided into rock block A, rock block B and rock block C, as proven in Fig. 2b. The deformation and failure of the roadway is set by the diploma of rotation and subsidence of the principle roof rock block A and the important thing block B. The coal pillar, the roadway roof and the stable coal aspect are the rock block A and B help our bodies, and the fracture place of the 2 has an vital affect on the power impact of the decrease help physique.
Mechanical evaluation of suspended roof gob-side entry roadway
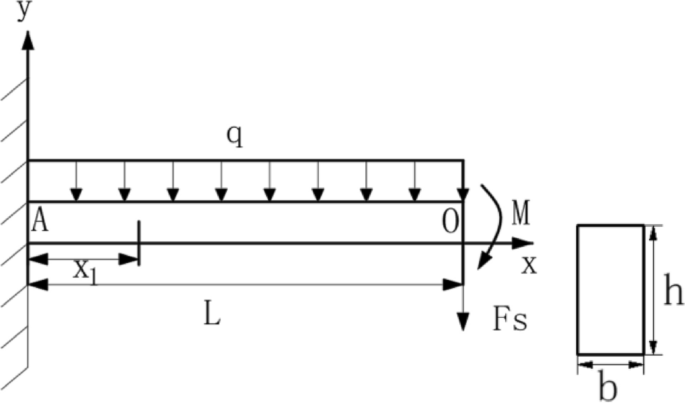
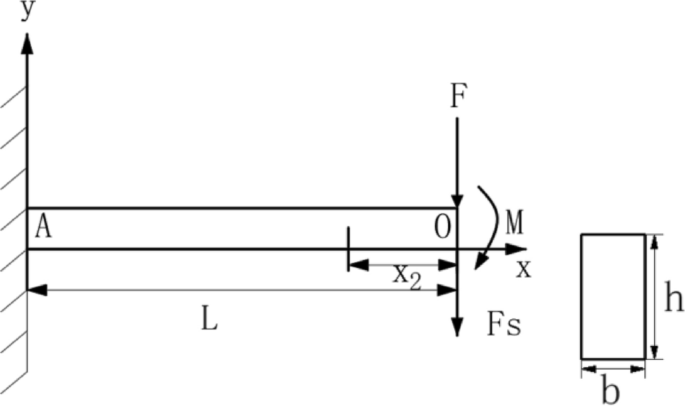
After the mining of the working face, the O-X collapse of the roof of the goaf happens, and the arc triangular block construction on each side of the working face is just not damaged. There’s nonetheless a sure suspended roof construction, which continues to bear the burden of the overburdened rock and continues to behave on the coal pillar and the roadway of the adjoining working face. So as to facilitate the evaluation of its beam construction, it may be merely considered a cantilever beam. The deep roof cantilever beam construction is especially affected by two elements of the load. The primary half is the rock mass load perpendicular to the highest of the hanging roof vary, and the opposite half is the partial hanging roof construction load that falls backward alongside the path of the caving angle, as proven in Fig. 3.
Roof caving and stress distribution in goaf.
As proven in Fig. 4, assuming that the common bulk density of the rock mass above every rock layer is γ and the dip angle of the coal seam is α, then the uniform load q is:
$$q = gamma bsumlimits_{1}^{n – 1} {H_{i} cos alpha }$$
(1)
the place:α is the dip angle of coal seam,°; n is the variety of rock strata from prime to backside; q is the uniform load of the rock layer above the hanging roof of the triangular block, N/m; Hi is the peak of the i layer above the roof, m; the common bulk density of γ-rock, N/m3.
Mechanical mannequin and power evaluation of cantilever beam construction.
Below the uniform load q, the bending second of the cantilever beam presently is:
$$M_{(x)} = qLx_{1} – frac{1}{2}qL^{2} – frac{1}{2}qx_{1}^{2} quad (0, leqslant ,x_{{1}} , < ,L)$$
(2)
the place:M is cantilever beam bending second, KN m; x1 is the gap from any level on L to the fastened finish A, m.
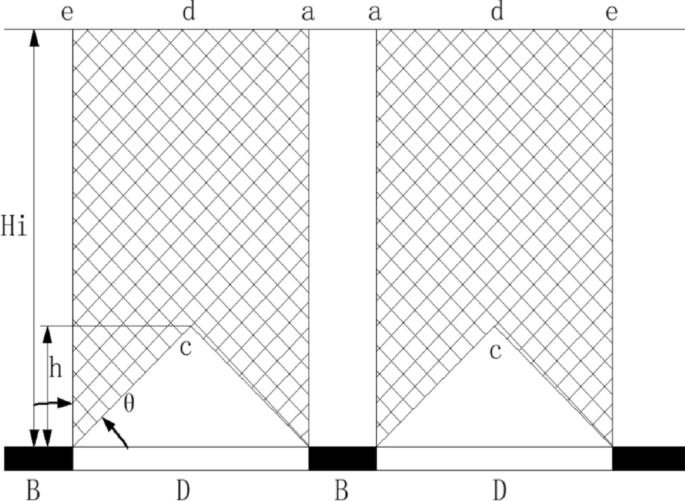
The load on the coal pillar of the roadway is brought on by the burden of the overburden rock on the coal pillar and the burden of the suspended strata on one or each side of the coal pillar transferred to the coal pillar, which is intently associated to the caving angle of the rock stratum. The caving angle of the rock stratum is the fracture of the roof of the goaf after reaching a sure hanging roof span. The fracture floor of every rock stratum is roughly situated on the identical straight line and its angle with the vertical path. The caving angle primarily will depend on the power of the coal physique. The coal physique has excessive power, good integrity, and a small caving angle, quite the opposite, the caving angle is massive. Due to this fact, we will calculate the burden of a part of the overburden rock carried by the coal pillar after the collapse of the rock stratum. As proven in Fig. 5, the overall load P on the coal pillar of 1 unit size is:
$$P = gamma bullet left[ {left( {B + D} right) bullet H – frac{{D^{2} {text{cot}}theta }}{{4}}} right]$$
(3)
the place:B is the width of coal pillar, m; D is the width of goaf, m; H is the buried depth of roadway, m; θ is the caving angle of overburden rock in goaf; h is the one layer thickness of the principle roof strata, m; γ is the common quantity power of overburden rock, kN/m3.
Calculation of coal pillar load diagram.
As proven in Fig. 6, in keeping with the Saint–Venant precept, the load imposed by the overburden rock inside this vary might be equal to making use of a concentrated power F on the finish of the cantilever beam:
$$F_{S} = F = frac{1}{2}gamma bhtan theta cos alpha left( {2 bullet sumlimits_{1}^{n – 1} {H_{i} – h} } proper)$$
(4)
the place:θ-rock collapse angle.
Mechanical mannequin and power evaluation of suspended roof construction.
The bending second equation is:
$$M_{(x)}^{prime } = Fx_{2} quad left( {0, < ,x_{{2}} , leqslant ,L} proper)$$
(5)
the place:M is cantilever beam bending second; x2 is the gap from any level on L to the fastened finish A.
In keeping with the superposition of the impact of the mechanical power of the fabric, the results of the mixed motion of a number of forces is equal to the sum of the outcomes of every power performing alone. Primarily based on this, it may be concluded that the utmost bending second of the hanging roof vertical overburden rock load and the overburden rock load within the caving zone to the triangular block hanging roof is:
$$start{aligned} M_{max } & = M_{{(x_{1} = 0)}} + M^{prime }_{{(x_{2} = L)}} & = frac{1}{2}gamma bLcos alpha left[ {left( {L + 2htan theta } right) bullet sumlimits_{1}^{n – 1} {H_{i} } – h^{2} tan theta } right] finish{aligned}$$
(6)
From the evaluation of the mechanical construction of the cantilever beam, the higher edge is subjected to tensile stress and the decrease edge is subjected to compressive stress. Mixed with rock mechanics, the compressive power of the rock is much larger than the tensile power, so in keeping with the utmost tensile power of the suspended roof, the last word caving step of the roof might be calculated.
$$start{aligned} sigma_{tmax } & = frac{{M_{max } y}}{{J_{Z} }} & = frac{3gamma cos alpha }{{h^{2} }}left[ {left( {L^{2} + 2Lhtan theta } right)sumlimits_{1}^{n – 1} {H_{i} } – Lh^{2} tan theta } right] finish{aligned}$$
(7)
the place: σtmax is the utmost tensile stress of the part, N/m2; y is the gap from the purpose to the impartial axis of the beam, taking half of the thickness of the speedy roof, m; JZ is the second of inertia, and the oblong part takes JZ = bh3/12; h is the thickness of speedy roof, m4.
The restrict caving step distance of the triangular block of the lateral suspended roof is solved as follows:
$$L = sqrt {h^{2} tan^{2} theta left( {1 – frac{h}{{2 bullet sumlimits_{1}^{n – 1} {H_{i} } }} + frac{{h^{2} }}{{4 bullet sumlimits_{1}^{n – 1} {H_{i}^{2} } }}} proper) + frac{{sigma_{tmax } h^{2} }}{{3gamma cos alpha sumlimits_{1}^{n – 1} {H_{i} } }}} + frac{{h^{2} tan theta }}{{2 bullet sumlimits_{1}^{n – 1} {H_{i} } }} – htan theta$$
(8)
Presently, the overburden load underneath the situation of the utmost span of the lateral suspension roof reaches the utmost:
$$start{aligned} Q_{1} & = gamma bLsumlimits_{1}^{n – 1} {H_{i} } cos alpha + frac{1}{2}gamma bhtan theta cos alpha left( {2 bullet sumlimits_{1}^{n – 1} {H_{i} – h} } proper) & = gamma bsumlimits_{1}^{n – 1} {H_{i} } cos alpha sqrt {h^{2} tan^{2} theta left( {1 – frac{h}{{2 bullet sumlimits_{1}^{n – 1} {H_{i} } }} + frac{{h^{2} }}{{4 bullet sumlimits_{1}^{n – 1} {H_{i}^{2} } }}} proper) + frac{{sigma_{tmax } h^{2} }}{{3gamma cos alpha sumlimits_{1}^{n – 1} {H_{i} } }}} finish{aligned}$$
(9)
The stress of the coal pillar after gob-side entry driving is especially composed of the rock mass above the decrease part roadway, the rock mass above the vertical coal pillar, the suspended roof of the goaf, and a few of the rock mass above. Now, the load of those rock plenty is analyzed:
The load of rock mass above the decrease part roadway is borne by the coal pillar and the stable coal of the decrease part mining face. Due to this fact, the central axis of the roadway is taken because the dividing level, and the load of rock mass above it’s borne by two elements. The half borne by the coal pillar is inclined because of the coal seam. The dip angle is α, after which half of the width of the divided central axis roadway is used to calculate the burden of the bearing rock mass:
$$Q_{2} = frac{{gamma bL_{1} sumlimits_{1}^{n} {H_{i} } cosalpha }}{2}$$
(10)
Equally, the load on the coal pillar by the overburden rock mass is:
$$Q_{3} = gamma bBsumlimits_{1}^{n} {H_{i}^{{}} } cos alpha$$
(11)
The restrict span of the hanging roof construction close to the goaf aspect of the coal pillar has been calculated earlier than. The load of the rock mass above the restrict span might be calculated in keeping with the components:
$$start{aligned} Q_{4} & = gamma bLsumlimits_{1}^{n} {H_{i} } cos alpha & = gamma bsumlimits_{1}^{n} {H_{i} } cos alpha left( {sqrt {h^{2} tan^{2} theta left( {1 – frac{h}{{2 bullet sumlimits_{1}^{n – 1} {H_{i} } }} + frac{{h^{2} }}{{4 bullet sumlimits_{1}^{n – 1} {H_{i}^{2} } }}} proper) + frac{{sigma_{tmax } h^{2} }}{{3gamma cos alpha sumlimits_{1}^{n – 1} {H_{i} } }}} + frac{{h^{2} tan theta }}{{2 bullet sumlimits_{1}^{n – 1} {H_{i} } }} – htan theta } proper) finish{aligned}$$
(12)
In the course of the roof of the goaf, it first breaks and collapses. The cantilever beam construction nonetheless bears the burden of the uncollapsed a part of the rock mass. The load is evenly distributed to the help our bodies on each side. The load of this a part of the rock mass might be calculated from the collapse angle θ presently:
$$Q_{5} = frac{1}{2}gamma bhtan theta cos alpha left( {2 bullet sumlimits_{1}^{n} {H_{i} – h} } proper)$$
(13)
Via the roof reducing know-how, the fracture line place of the essential roof is artificially managed, and the overburden construction is improved to make the higher a part of the roadway and the essential roof rock block of the goaf disconnect with out forming a construction. The suspended roof construction collapses alongside the reducing line to cut back the lateral stress impact of the lateral suspended roof on the roadway and coal pillar. If the collapse angle is θ1 presently, it may be seen from the burden evaluation of the overburden rock mass that the burden of the suspended roof after the roof reducing is:
$$Q_{5}^{prime } = frac{1}{2}gamma bhtan theta_{1} cos alpha left( {2 bullet sumlimits_{1}^{n} {H_{i} – h} } proper)$$
(14)
The bearing capability of coal pillar after roof reducing is:
$$start{aligned} Q & = Q_{2} + Q_{3} + Q_{5}^{prime } & = frac{gamma b cos alpha }{2}left[ {left( {2htan theta_{1} + L_{1} + 2B} right) bullet sumlimits_{1}^{n} {H_{i} – h^{2} tan theta_{1} } } right] finish{aligned}$$
(15)
The discount relative to the pre-cut prime is:
$$start{aligned}Q & = Q_{4} + Q_{5} – Q_{5}^{prime } & = gamma bcos alpha left[ sumlimits_{1}^{n} {H_{i} left({sqrt {h^{2} tan^{2} theta left( {1 – frac{h}{{2 bulletsumlimits_{1}^{n – 1} {H_{i} } }} + frac{{h^{2} }}{{4 bulletsumlimits_{1}^{n – 1} {H_{i}^{2} } }}} right) +frac{{sigma_{tmax } h^{2} }}{{3gamma cos alphasumlimits_{1}^{n – 1} {H_{i} } }}} + frac{{h^{2} tan theta}}{{2 bullet sumlimits_{1}^{n – 1} {H_{i} } }} – htan theta }right)} right. &quadleft.+ htan theta left( {sumlimits_{1}^{n} {H_{i} – 2h} }right) right] finish{aligned}$$
(16)
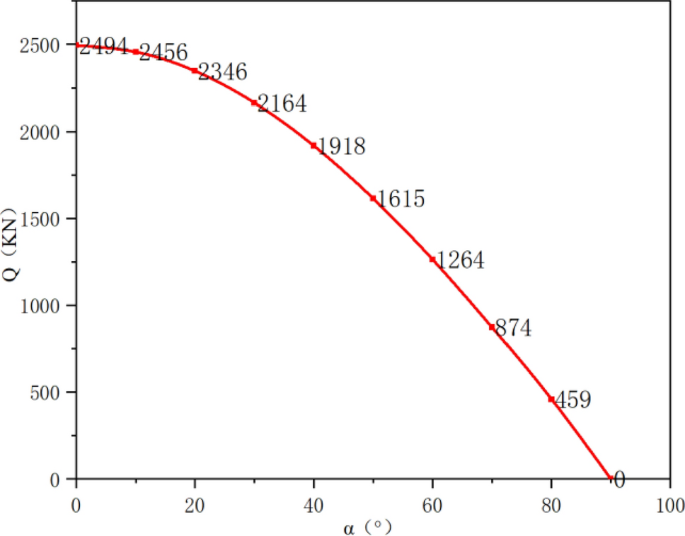
So as to get hold of the affect of coal seam dip angle on the discount of coal pillar bearing capability earlier than and after roof reducing, the discount of coal pillar bearing capability similar to totally different coal seam dip angles is calculated in keeping with Components (16). The calculation parameters are chosen in keeping with the mechanical parameters of the rock strata given within the geological information of the 230,708 working face of Huopu Mine. The γ is 14.21 kN/m3, the thickness of the speedy roof is 2.2 m, the thickness of the principle roof is 6.6 m, and the unit physique b is 1. In keeping with the literature32,33, θ is 63°. The calculation outcomes are proven in Fig. 7. With the rise of the dip angle of the coal seam, the discount of the bearing capability of the coal pillar earlier than the comparative roof reducing is steadily decreased to zero.
Discount of coal pillar bearing capability with coal seam dip angle earlier than and after roof reducing.
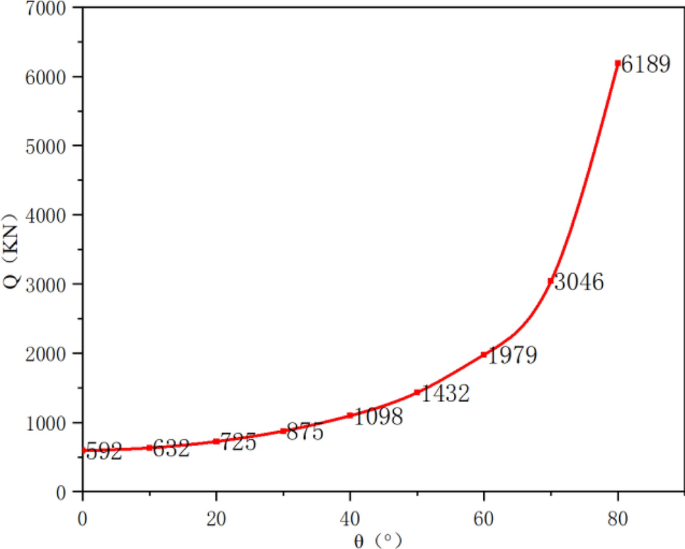
So as to get hold of the affect of the caving angle of the overburden rock on the discount of the bearing capability of the coal pillar earlier than and after the roof reducing, the discount of the bearing capability of the coal pillar similar to the totally different caving angles of the overburden rock is calculated in keeping with the components (16). The calculation parameters are chosen in keeping with the mechanical parameters of the rock strata given within the geological information of the 230,708 working face of Huopu Mine. The γ is 14.21 kN/m3, the thickness of the speedy roof is 2.2 m, the thickness of the principle roof is 6.6 m, the α is 30°, and the unit physique b is 1. The calculation outcomes are proven in Fig. 8. With the rise of the caving angle of the overburden rock, the discount of the bearing capability of the coal pillars earlier than the comparative roof reducing continues to extend.
Discount of coal pillar bearing capability with caving angle earlier than and after roof reducing.
